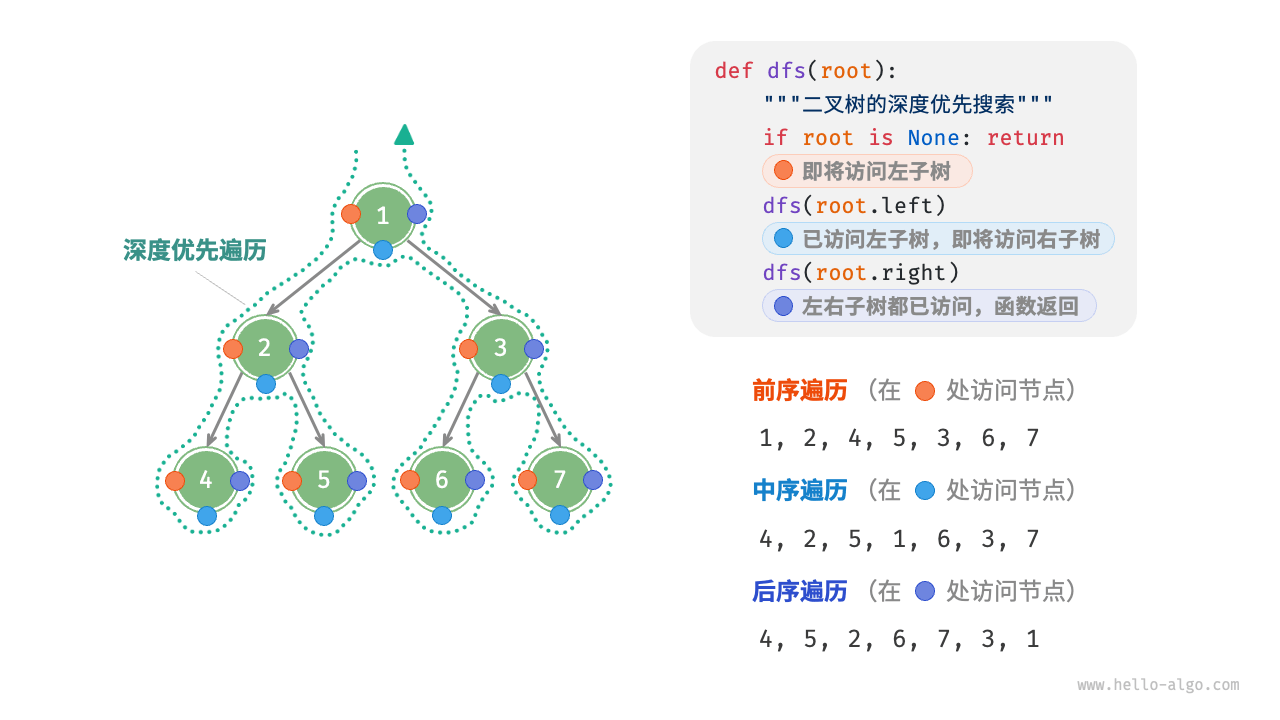
二叉树的建立与遍历 二叉树是一种非线性数据结构. 二叉树 由节点构成,每个节点包含节点值和指向左节点和右节点的指针.常用术语: 根节点（root node）：位于二叉树顶层的节点，没有父节点。叶节点（leaf node）：没有子节点的节点，其两个指针均指向 None 。边（edge）：连接两个节点的线段，即节点引用（指针）。节点所在的层（level）：从顶至底递增，根节点所在层为 1 。节点的度（degree）：节点的子节点的数量。在二叉树中，度的取值范围是 0、1、2 。二叉树的高度（height）：从根节点到最远叶节点所经过的边的数量。节点的深度（depth）：从根节点到该节点所经过的边的数量。节点的高度（height）：从距离该节点最远的叶节点到该节点所经过的边的数量。二叉树的遍历 分为层序遍历,前序遍历,中序遍历,后序遍历.层序遍历本质为BFS,即广度优先搜索.层序遍历顾名思义,为一层层的从上往下,从左到右遍历.前序遍历,中序遍历,后序遍历本质为DFS,即深度优先搜索.访问时机如图: 代码示例:#include<vector> #include<queue> #include<iostream> struct tree{ int value; tree *left; tree *right; tree(int x) : value(x), left(nullptr), right(nullptr){} }; std::vector<int> vec; //层序遍历 std::vector<int> levelorder(tree *root){ std::queue<tree *> q; q.push(root); std::vector<int> vec; while(!q.empty()){ tree *node = q.front(); q.pop(); vec.push_back(node->value); if(node->left != nullptr){ q.push(node->left); } if(node->right != nullptr){ q.push(node->right); } } return vec; } //前序遍历 void preorder(tree *root){ if(root == nullptr){ return; } vec.push_back(root->value); preorder(root->left); preorder(root->right); } //中序遍历 void inorder(tree *root){ if(root == nullptr){ return; } inorder(root->left); vec.push_back(root->value); inorder(root->right); } //后序遍历 void postorder(tree *root){ if(root == nullptr){ return; } postorder(root->left); postorder(root->right); vec.push_back(root->value); } int main(){ tree *t0 = new tree(1); tree *t1 = new tree(2); tree *t2 = new tree(3); tree *t3 = new tree(4); tree *t4 = new tree(5); t0->left = t1; t0->right = t2; t1->left = t3; t1->right = t4; preorder(t0); for(auto &i : vec){ std::cout << i << " "; } std::cout << std::endl; vec.clear(); inorder(t0); for(auto &i : vec){ std::cout << i << " "; } std::cout << std::endl; vec.clear(); postorder(t0); for(auto &i : vec){ std::cout << i << " "; } std::cout << std::endl; vec.clear(); return 0; }使用数组表示二叉树: 用数组表示时,观察可知节点下标为 i 时,父节点下标为 (i - 1) / 2 左节点下标为 2 i + 1 ,右节点下标为 2 i + 2 依此规律我们可以使用数组表示出二叉树#include<vector> #include<iostream> std::vector<int> vec; int parent(int i){ return (i - 1) / 2; } int left(int i){ return 2 * i + 1; } int right(int i){ return 2 * i + 2; } void pretree(std::vector<int> &tree, int i){ if(i < 0 || i >= tree.size()){ return; } vec.push_back(tree[i]); pretree(tree, left(i)); pretree(tree, right(i)); } void intree(std::vector<int> &tree, int i){ if(i < 0 || i >= tree.size()){ return; } intree(tree, left(i)); vec.push_back(tree[i]); intree(tree, right(i)); } void posttree(std::vector<int> &tree, int i){ if(i < 0 || i >= tree.size()){ return; } posttree(tree, left(i)); posttree(tree, right(i)); vec.push_back(tree[i]); } int main(){ std::vector<int> tree(10); for(int i = 0; i < 10; i++){ std::cin >> tree[i]; } pretree(tree, 0); for(auto &i : vec){ std::cout << i << " "; } std::cout << std::endl; vec.clear(); intree(tree, 0); for(auto &i : vec){ std::cout << i << " "; } std::cout << std::endl; vec.clear(); posttree(tree, 0); for(auto &i : vec){ std::cout << i << " "; } std::cout << std::endl; vec.clear(); return 0; }参考文章

链表 链表是一种逻辑结构上的线性表，物理结构上的非线性表链表由许多节点组成，每个节点有对应的值和指向下一个节点的指针第一个节点称为首节点，最后一个节点称为尾节点，尾节点的指向为空.特点:查找某一节点都是由头开始遍历查找，增加节点的效率比顺序表快，删除节点的效率比顺序表快，查找节点的效率比顺序表慢代码示例:#include<iostream> using namespace std; //创建链表结构体,数据成员有值和指向下一节点的指针 struct list{ int value; list *next; list(int x){ value = x; next = nullptr; } }; //在n节点后插入p节点 void insert(list *n, list *p){ p->next = n->next; n->next = p; } //删除n节点的下一个节点 void remove(list *n){ if(n->next == nullptr){ return; } list *p = n->next; list *n1 = p->next; n->next = n1; delete p; } //访问索引index的节点 list *access(list *head, int index){ for(int i = 0; i < index; i++){ if(head == nullptr){ return nullptr; } head = head->next; } return head; } //查找值为target的节点,输出索引 int find(list *head, int target){ int index = 0; while(head != nullptr){ if(head->value == target){ return index; } head = head->next; index++; } return -1; } int main(){ //创建节点 list *n1 = new list(1); list *n2 = new list(2); list *n3 = new list(3); //连接节点 n1->next = n2; n2->next = n3; //测试函数 list *p = new list(10); insert(n1, p); remove(n2); list *p1 = access(n1, 1); cout << find(n1, 10) << endl; return 0; }

C++实现顺序表 顺序表,一种线性表,因此顺序表是线性的.因为顺序表在物理结构与逻辑结构都是连续的.意味着在内存中是连续存储的,形如数组的内存存储方式,我将用数组实现顺序表.实现顺序表的主要功能为:增删查改.顺序表是一种简单的数据结构,原理与实现并不难主要维护下标size,内存空间capacity的大小即可Seqlist.h头文件声明#pragma once #include<iostream> #include<cstdlib> #include<cassert> using namespace std; // 顺序表结构定义 typedef int SLDataType; class SeqList { public: SLDataType* arr; int size; int capacity; }; typedef SeqList SL; //检查顺序表容量是否合理 void checkSLCaoacity(SL* ps); //顺序表初始化 void SLInit(SL* ps); //顺序表的销毁 void SLDestroy(SL* ps); //顺序表的插入操作 //头插尾插 void SLPushFront(SL* ps,SLDataType x); void SLPushBack(SL* ps, SLDataType x); //头删尾删 void SLPopFront(SL* ps); void SLPopBack(SL* ps); //选择插入 void SLInsert(SL* ps,int i, SLDataType x); //选择删除 void SLDelete(SL* ps, SLDataType x); //顺序表的查找操作 void SLFind(SL* ps, SLDataType x); //顺序表的修改操作 void SLUpdate(SL* ps, int i, SLDataType x); //输出所以元素 void SLPrint(SL* ps);Seqlist.cpp原文件中存方法#include"SeqList.h" void SLInit(SL* ps) { ps->arr = NULL; ps->size=ps->capacity=0; } void SLDestroy(SL* ps) { if (ps->arr) { delete[] ps->arr; } ps->arr = NULL; ps->size = ps->capacity = 0; } void checkSLCaoacity(SL* ps) { //先判断空间够不够 if (ps->size == ps->capacity) { int newCapacity = (ps->capacity == 0) ? sizeof(SLDataType) : 2 * ps->capacity; SLDataType* temp = (SLDataType*)realloc(ps->arr, newCapacity * sizeof(SLDataType)); if (!temp) { perror("realloc failed"); exit(1); } ps->arr = temp; //delete(temp); ps->capacity = newCapacity; } } //头插尾插 void SLPushFront(SL* ps, SLDataType x) { assert(ps);//传其他类型指针会导致崩溃，给爷爬 checkSLCaoacity(ps); //插入 for (int i = ps->size; i > 0; i--) { ps->arr[i] = ps->arr[i - 1]; } ps->arr[0] = x; ps->size++; } void SLPushBack(SL* ps, SLDataType x) { assert(ps); checkSLCaoacity(ps); ps->arr[ps->size++] = x; } //头删尾删 void SLPopFront(SL* ps) { assert(ps); if (ps->size == 0) { return; } for (int i = 0; i < (ps->size--) - 1; i++) { ps->arr[i + 1] = ps->arr[i]; } } void SLPopBack(SL* ps) { assert(ps); if (ps->size == 0) { return; } ps->size--; } //选择插入 void SLInsert(SL* ps, int i, SLDataType x) { assert(ps); checkSLCaoacity(ps); //1 2 3 4 5 size //0 1 2 3 4 for (int j = ps->size; j >i; j--) { ps->arr[j] = ps->arr[j - 1]; } ps->arr[i] = x; ps->size++; } //选择删除 void SLDelete(SL* ps, SLDataType x) { assert(ps); if (ps->size == 0) { return; } for (int j = 0; j < ps->size; j++) { if (ps->arr[j] == x) { for (int k = j; k < ps->size - 1; k++) { ps->arr[k] = ps->arr[k + 1]; } ps->size--; return; } } cout << "没有找到要删除的元素" << '\n'; } //顺序表的查找操作 void SLFind(SL* ps, SLDataType x) { assert(ps); for (int i = 0; i <= ps->size - 1; i++) { if (ps->arr[i] == x) { cout << "找到了第" << i + 1 << "个元素\n"; cout << "值为:" << ps->arr[i] << '\n'; return; } } cout << "没有找到要查找的元素" << '\n'; } //顺序表的修改操作 void SLUpdate(SL* ps, int i, SLDataType x) { assert(ps); checkSLCaoacity(ps); if (i <= 0 || i > ps->size - 1) { cout << "索引越界" << '\n'; return; } ps->arr[i - 1] = x; } //输出所有元素 void SLPrint(SL* ps) { assert(ps); checkSLCaoacity(ps); for (int i = 0; i < ps->size; i++) { cout << ps->arr[i] << " "; } cout << '\n'; }test.cpp源文件中用于测试实现的功能#include"SeqList.h" void test01() { SL s; SLInit(&s);//初始化 //增删查改 //使用for循环插入100个元素 for (int i = 1; i <= 100; i++) { if(i&1) SLPushFront(&s, i); else SLPushBack(&s, i); } //输出所有元素 SLPrint(&s); //查找元素 SLFind(&s, 55); SLFind(&s, 999); //删除元素 SLDelete(&s, 100); SLDelete(&s, 404); SLPrint(&s); //修改元素 SLUpdate(&s, 55, 969696); SLPrint(&s); SLDestroy(&s);//销毁 } int main() { test01(); return 0; }