搜索到
27
篇与
的结果
-
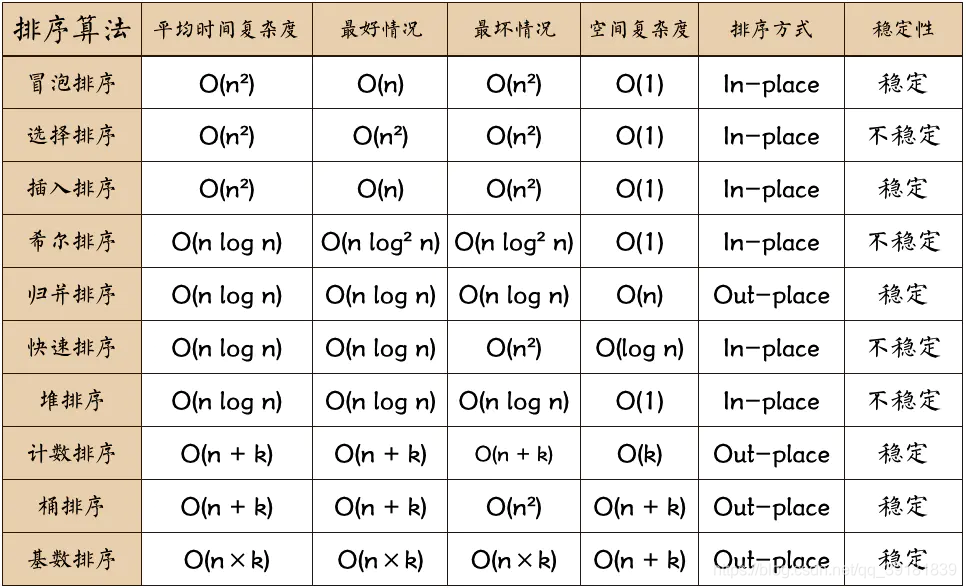
 排序算法 一.插入排序(Insertion Sort) 插入排序,如打扑克时的理牌一样,左手为空,从牌堆摸牌,将摸到的牌从右往左对比,放到比其小的牌的右边。代码示例:#include<iostream> using namespace std; int main() { int a[10]; for (int i = 0; i < 10; i++) { cin >> a[i]; } //4 5 2 8 1 9 3 7 6 0 a数组的key //0 1 2 3 4 5 6 7 8 9 i下标 for (int i = 2; i < 10; i++) { int key = a[i];//选定一个数将其与左边的数一一对比 int j = i - 1; while (j >= 0 && a[j] < key) //如果比选定的数字大则将其右移 { a[j + 1] = a[j]; j--; } a[j + 1] = key; } for (int i = 0; i < 10; i++) { cout << a[i] << " "; } return 0; }二.选择排序(Selection sort) 遍历数组,找到最小的数,交换位置,让最小的数排在前面代码示例:#include<iostream> using namespace std; int main() { int a[10]; for (int i = 0; i < 10; i++)cin >> a[i]; for (int i = 0; i < 10; i++) { int temp = i; for (int j = i; j < 10; j++) { if (a[j] < a[temp]) { temp = j; } } swap(a[i], a[temp]); } for (int i = 0; i < 10; i++) { cout << a[i] << " "; } return 0; }三.冒泡排序(Bubble Sort) 每次就行两个数之间的比较,将大(小)的数放在右边,每次循环更大(小)的数会像泡泡一样飘到最右边.代码示例:#include<iostream> using namespace std; int main() { // 定义包含10个元素的整数数组 int a[10]; for (int i = 0; i < 10; i++) { // 从标准输入流读取用户输入的整数,并存储到数组a中 cin >> a[i]; } // 使用冒泡排序算法对数组a进行排序 for (int i = 0; i < 10; i++) { for (int j = i + 1; j < 10; j++) { // 如果当前元素大于后续元素,则交换它们的位置 if (a[i] > a[j]) { int temp=a[i]; a[i] = a[j]; a[j] = temp; } } } // 输出排序后的数组a for (int i = 0; i < 10; i++) { cout << a[i] << " "; } // 返回程序运行成功状态 return 0; } 四.合并排序(Merge sort) 利用递归,将原数组拆分,接着合并的同时排序,如图 代码示例:#include<iostream> #include<vector> using namespace std; // 归并排序的辅助函数,用于将两个已排序的子数组合并为一个排序数组 void merge(vector<int>& a, int l, int mid, int r) { int nx = mid - l + 1; // 计算第一个子数组的大小 int ny = r - mid; // 计算第二个子数组的大小 vector<int>P(nx); // 创建第一个子数组 vector<int>Q(ny); // 创建第二个子数组 // 将元素复制到临时数组P和Q中 for (int i = 0; i < nx; i++) { P[i] = a[l + i]; } for (int i = 0; i < ny; i++) { Q[i] = a[mid + 1 + i]; } int i = 0, j = 0, k = l; // 合并两个子数组 while (i < nx && j < ny) { if (P[i] <= Q[j]) { a[k] = P[i]; i++; } else { a[k] = Q[j]; j++; } k++; } // 将剩余的元素复制回原数组 while (i < nx) { a[k] = P[i]; i++; k++; } while (j < ny) { a[k] = Q[j]; j++; k++; } } // 归并排序算法的主要逻辑,递归地将数组分为较小的数组,并调用merge函数进行合并 void merge_sort(vector<int>& a, int l, int r) { if (l < r) { int mid = (l + r) / 2; // 计算中间索引 merge_sort(a, l, mid); // 递归排序左半部分 merge_sort(a, mid + 1, r); // 递归排序右半部分 merge(a, l, mid, r); // 合并两个已排序的子数组 } } int main() { vector<int>a(10); // 创建一个包含10个元素的向量 // 从标准输入中读取输入元素并存储在向量中 for (int i = 0; i < 10; i++) { cin >> a[i]; } merge_sort(a, 0, a.size() - 1); // 对输入的数组进行归并排序 // 输出排序后的数组元素 for (int i = 0; i < 10; i++) { cout << a[i] << " "; } return 0; } 五.快速排序(Quick Sort) 快速排序维护左右指针left,right和基准点base 先让right不断向左扫,找到比base大(小)的值然后与left指向的值交换 然后left不断向右扫,找到比base小(大)的值然后与right指向的值交换 一次操作后会形成两个区间,然后分别对两个区间进行上述操作 代码示例中用了两种方法,一种普通的,一种使用分治代码示例:#include<iostream> using namespace std; void quickSort_num1(int arr[], int star, int end) { //确定左右指针的位置 int left = star, right = end; //设置基准点 int base = arr[star]; if (left < right) { while (left < right) { //先让由指针不断往左寻找比 base 小的值,找到了便交换 //如果没找到,此时left = right 等于没交换 while (left < right && arr[right] >= base) { right--; } arr[left] = arr[right]; //先让由指针不断往右寻找比 base 大的值,找到了便交换 //如果没找到,此时left = right 等于没交换 while (left < right && arr[left] <= base) { left++; } arr[right] = arr[left]; } //arr[right] = base 也可以,因为最终left=right arr[left] = base; //接着再让分割好的两个小区间进行上述操作 //左边区间为比base小的值 quickSort_num1(arr, star, left - 1); //右边区间为比base大的值 quickSort_num1(arr, left + 1, end); } } //采用分治的方法,先找分割点 //partition为寻找分割点的函数 int partition(int arr[], int left, int right) { int base = arr[left]; while (left < right) { //先让由指针不断往左寻找比 base 小的值,找到了便交换 //如果没找到,此时left = right 等于没交换 while (left < right && arr[right] >= base) { right--; } arr[left] = arr[right]; //先让由指针不断往右寻找比 base 大的值,找到了便交换 //如果没找到,此时left = right 等于没交换 while (left < right && arr[left] <= base) { left++; } arr[right] = arr[left]; } arr[left] = base; return left; } void quickSort_num2(int arr[], int left, int right) { if (left < right) { //确定分割点 int pos = partition(arr, left, right); //左右区间,再重复操作 quickSort_num2(arr, left, pos - 1); quickSort_num2(arr, pos + 1, right); } } int main() { int arr1[10] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 10}; quickSort_num1(arr1, 0, 9); for (int i = 0; i < 10; i++) { cout << arr1[i] << " "; } cout << '\n'; //采用分治思想 int arr2[10] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 10}; quickSort_num2(arr2, 0, 9); for (int i = 0; i < 10; i++) { cout << arr2[i] << " "; } cout << '\n'; return 0; }
排序算法 一.插入排序(Insertion Sort) 插入排序,如打扑克时的理牌一样,左手为空,从牌堆摸牌,将摸到的牌从右往左对比,放到比其小的牌的右边。代码示例:#include<iostream> using namespace std; int main() { int a[10]; for (int i = 0; i < 10; i++) { cin >> a[i]; } //4 5 2 8 1 9 3 7 6 0 a数组的key //0 1 2 3 4 5 6 7 8 9 i下标 for (int i = 2; i < 10; i++) { int key = a[i];//选定一个数将其与左边的数一一对比 int j = i - 1; while (j >= 0 && a[j] < key) //如果比选定的数字大则将其右移 { a[j + 1] = a[j]; j--; } a[j + 1] = key; } for (int i = 0; i < 10; i++) { cout << a[i] << " "; } return 0; }二.选择排序(Selection sort) 遍历数组,找到最小的数,交换位置,让最小的数排在前面代码示例:#include<iostream> using namespace std; int main() { int a[10]; for (int i = 0; i < 10; i++)cin >> a[i]; for (int i = 0; i < 10; i++) { int temp = i; for (int j = i; j < 10; j++) { if (a[j] < a[temp]) { temp = j; } } swap(a[i], a[temp]); } for (int i = 0; i < 10; i++) { cout << a[i] << " "; } return 0; }三.冒泡排序(Bubble Sort) 每次就行两个数之间的比较,将大(小)的数放在右边,每次循环更大(小)的数会像泡泡一样飘到最右边.代码示例:#include<iostream> using namespace std; int main() { // 定义包含10个元素的整数数组 int a[10]; for (int i = 0; i < 10; i++) { // 从标准输入流读取用户输入的整数,并存储到数组a中 cin >> a[i]; } // 使用冒泡排序算法对数组a进行排序 for (int i = 0; i < 10; i++) { for (int j = i + 1; j < 10; j++) { // 如果当前元素大于后续元素,则交换它们的位置 if (a[i] > a[j]) { int temp=a[i]; a[i] = a[j]; a[j] = temp; } } } // 输出排序后的数组a for (int i = 0; i < 10; i++) { cout << a[i] << " "; } // 返回程序运行成功状态 return 0; } 四.合并排序(Merge sort) 利用递归,将原数组拆分,接着合并的同时排序,如图 代码示例:#include<iostream> #include<vector> using namespace std; // 归并排序的辅助函数,用于将两个已排序的子数组合并为一个排序数组 void merge(vector<int>& a, int l, int mid, int r) { int nx = mid - l + 1; // 计算第一个子数组的大小 int ny = r - mid; // 计算第二个子数组的大小 vector<int>P(nx); // 创建第一个子数组 vector<int>Q(ny); // 创建第二个子数组 // 将元素复制到临时数组P和Q中 for (int i = 0; i < nx; i++) { P[i] = a[l + i]; } for (int i = 0; i < ny; i++) { Q[i] = a[mid + 1 + i]; } int i = 0, j = 0, k = l; // 合并两个子数组 while (i < nx && j < ny) { if (P[i] <= Q[j]) { a[k] = P[i]; i++; } else { a[k] = Q[j]; j++; } k++; } // 将剩余的元素复制回原数组 while (i < nx) { a[k] = P[i]; i++; k++; } while (j < ny) { a[k] = Q[j]; j++; k++; } } // 归并排序算法的主要逻辑,递归地将数组分为较小的数组,并调用merge函数进行合并 void merge_sort(vector<int>& a, int l, int r) { if (l < r) { int mid = (l + r) / 2; // 计算中间索引 merge_sort(a, l, mid); // 递归排序左半部分 merge_sort(a, mid + 1, r); // 递归排序右半部分 merge(a, l, mid, r); // 合并两个已排序的子数组 } } int main() { vector<int>a(10); // 创建一个包含10个元素的向量 // 从标准输入中读取输入元素并存储在向量中 for (int i = 0; i < 10; i++) { cin >> a[i]; } merge_sort(a, 0, a.size() - 1); // 对输入的数组进行归并排序 // 输出排序后的数组元素 for (int i = 0; i < 10; i++) { cout << a[i] << " "; } return 0; } 五.快速排序(Quick Sort) 快速排序维护左右指针left,right和基准点base 先让right不断向左扫,找到比base大(小)的值然后与left指向的值交换 然后left不断向右扫,找到比base小(大)的值然后与right指向的值交换 一次操作后会形成两个区间,然后分别对两个区间进行上述操作 代码示例中用了两种方法,一种普通的,一种使用分治代码示例:#include<iostream> using namespace std; void quickSort_num1(int arr[], int star, int end) { //确定左右指针的位置 int left = star, right = end; //设置基准点 int base = arr[star]; if (left < right) { while (left < right) { //先让由指针不断往左寻找比 base 小的值,找到了便交换 //如果没找到,此时left = right 等于没交换 while (left < right && arr[right] >= base) { right--; } arr[left] = arr[right]; //先让由指针不断往右寻找比 base 大的值,找到了便交换 //如果没找到,此时left = right 等于没交换 while (left < right && arr[left] <= base) { left++; } arr[right] = arr[left]; } //arr[right] = base 也可以,因为最终left=right arr[left] = base; //接着再让分割好的两个小区间进行上述操作 //左边区间为比base小的值 quickSort_num1(arr, star, left - 1); //右边区间为比base大的值 quickSort_num1(arr, left + 1, end); } } //采用分治的方法,先找分割点 //partition为寻找分割点的函数 int partition(int arr[], int left, int right) { int base = arr[left]; while (left < right) { //先让由指针不断往左寻找比 base 小的值,找到了便交换 //如果没找到,此时left = right 等于没交换 while (left < right && arr[right] >= base) { right--; } arr[left] = arr[right]; //先让由指针不断往右寻找比 base 大的值,找到了便交换 //如果没找到,此时left = right 等于没交换 while (left < right && arr[left] <= base) { left++; } arr[right] = arr[left]; } arr[left] = base; return left; } void quickSort_num2(int arr[], int left, int right) { if (left < right) { //确定分割点 int pos = partition(arr, left, right); //左右区间,再重复操作 quickSort_num2(arr, left, pos - 1); quickSort_num2(arr, pos + 1, right); } } int main() { int arr1[10] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 10}; quickSort_num1(arr1, 0, 9); for (int i = 0; i < 10; i++) { cout << arr1[i] << " "; } cout << '\n'; //采用分治思想 int arr2[10] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 10}; quickSort_num2(arr2, 0, 9); for (int i = 0; i < 10; i++) { cout << arr2[i] << " "; } cout << '\n'; return 0; } -
 单调栈 (单调栈模板题)题目描述给定一个长度为n的整数数组a,你需要求出每个元素的左边离它最近且比它小的元素。输入描述第一行:一个整数n(1≤n≤2×10^5)第二行:n个整数,表示整数数组a.(1≤a≤10^9)输出描述共一行,n个整数,表示每个元素的左边第一个比它小的元素,若不存在则为−1。输入样例157 8 5 6 7输出样例1-1 7 -1 5 6我们可以使用STL中的stack实现思路主要为将数组中的数值于栈中的数值进行对比,但栈中的数组比数组中的值大时,我们需要舍弃栈中的数,否则将数组中的值压入栈中代码示例:#include<iostream> #include<stack> using namespace std; const int N = 2e5; int a[N], b[N]; int main() { std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n; cin >> n; for (int i = 1; i <= n; i++)cin >> a[i]; stack<int>q; for (int i = 1; i <= n; i++) { while (!q.empty() && q.top() >= a[i])q.pop(); if (q.empty())b[i] = -1; else b[i] = q.top(); q.push(a[i]); } for (int i = 1; i <= n; i++)cout << b[i] << " "; return 0; }使用stack是一种选择,但是更推荐使用数组模拟来实现单调栈,因为数组能进行更多操作,对于题目的适应与灵活度更高。但是因为数组空间固定要注意数组栈的溢出问题。下面给出数组实现的代码:#include<iostream> using namespace std; const int N = 2e5; int a[N], b[N], stk[N], top; int main() { std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n; cin >> n; for (int i = 1; i <= n; i++)cin >> a[i]; for (int i = 1; i <= n; i++) { while (top && a[stk[top]] >= a[i])top--; if (top)b[i] = a[stk[top]]; else b[i] = -1; stk[++top] = i; } for (int i = 1; i <= n; i++)cout << b[i] << " "; return 0; }
单调栈 (单调栈模板题)题目描述给定一个长度为n的整数数组a,你需要求出每个元素的左边离它最近且比它小的元素。输入描述第一行:一个整数n(1≤n≤2×10^5)第二行:n个整数,表示整数数组a.(1≤a≤10^9)输出描述共一行,n个整数,表示每个元素的左边第一个比它小的元素,若不存在则为−1。输入样例157 8 5 6 7输出样例1-1 7 -1 5 6我们可以使用STL中的stack实现思路主要为将数组中的数值于栈中的数值进行对比,但栈中的数组比数组中的值大时,我们需要舍弃栈中的数,否则将数组中的值压入栈中代码示例:#include<iostream> #include<stack> using namespace std; const int N = 2e5; int a[N], b[N]; int main() { std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n; cin >> n; for (int i = 1; i <= n; i++)cin >> a[i]; stack<int>q; for (int i = 1; i <= n; i++) { while (!q.empty() && q.top() >= a[i])q.pop(); if (q.empty())b[i] = -1; else b[i] = q.top(); q.push(a[i]); } for (int i = 1; i <= n; i++)cout << b[i] << " "; return 0; }使用stack是一种选择,但是更推荐使用数组模拟来实现单调栈,因为数组能进行更多操作,对于题目的适应与灵活度更高。但是因为数组空间固定要注意数组栈的溢出问题。下面给出数组实现的代码:#include<iostream> using namespace std; const int N = 2e5; int a[N], b[N], stk[N], top; int main() { std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n; cin >> n; for (int i = 1; i <= n; i++)cin >> a[i]; for (int i = 1; i <= n; i++) { while (top && a[stk[top]] >= a[i])top--; if (top)b[i] = a[stk[top]]; else b[i] = -1; stk[++top] = i; } for (int i = 1; i <= n; i++)cout << b[i] << " "; return 0; } -
 (BFS) Breadth-First Search入门 广度优先搜索:BFS全称Breadth First Search.广度优先,优先在于广度,尽量的往周围扩散再前进。如果是DFS是一只迷宫里的蚂蚁,那么BFS就像倒在地上的一滩水.BFS的搜索是蔓延式的进行.观察下列,搜索是从(1,1)开始的 搜索的优先级为右下左上 每个数字代表是第几个被搜索到的1 2 4 7 113 5 8 12 166 9 13 17 2010 14 18 21 2315 19 22 24 25可以观察到我们的搜索是如水一般蔓延开来的,按照我们设置好的搜索规则依次判断.我们设置了一个边长为5X5的图,且初始点我们让其从(1,1)开始进行.过程的简单描述:从(1,1)开始,先判断右边是否走过,没走过将其标为2.然后再回到(1,1)接着判断下面是否走过,没走过将其标为3.然后判断左边,为边界无法走,接着判断上面,为边界无法走.(1,1)此时4个方位都判断完了,接着来到(1,1)这个点判断标记的第一个点———(1,2)然后从(1,2)开始刚刚的过程,最终形成了这个图.题目:快乐的马里奥 这是一个基础的bfs题,题解思路如我们上述相同. 用代码怎么实现呢? 我们需要用到核心为 queue 和 pair 使用队列的特性---先进先出,记录最先标记了的坐标位置,下面给出AC代码#include<iostream> #include<queue> #include<vector> using namespace std; int fx[4]={0,1,0,-1}; int fy[4]={1,0,-1,0}; int main() { std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); int m, n; cin >> m >> n;//输入行列 vector<vector <int> >v( m + 1,vector<int> ( n + 1, 0 ));//设置二维数组 queue<pair<int,int> >q;//队列用来记录坐标 q.push({1,1});//设置初始的坐标,也是开始的坐标 v[1][1] = 1;//对初始点赋初值 int cnt = 2;//因为初始点为1,第二个点从2开始 while(!q.empty()){//队列存储的坐标不为空就执行 //取出队列中存储的第一个坐标,用完就丢 int x = q.front().first; int y = q.front().second; q.pop(); //依次判断四个方位 for(int i = 0;i < 4;i++){ int nx = x + fx[i]; int ny = y + fy[i]; if(nx <= m && nx > 0 && ny <= n && ny > 0 && v[nx][ny] == 0){ v[nx][ny] = cnt++;//赋值标记 q.push({nx,ny});//将赋值点的坐标存入队列 } } } //打印输出 for(int i = 1; i <= m;i++){ for(int j = 1; j <= n;j++){ cout << v[i][j] << " "; } cout << '\n'; } return 0; }
(BFS) Breadth-First Search入门 广度优先搜索:BFS全称Breadth First Search.广度优先,优先在于广度,尽量的往周围扩散再前进。如果是DFS是一只迷宫里的蚂蚁,那么BFS就像倒在地上的一滩水.BFS的搜索是蔓延式的进行.观察下列,搜索是从(1,1)开始的 搜索的优先级为右下左上 每个数字代表是第几个被搜索到的1 2 4 7 113 5 8 12 166 9 13 17 2010 14 18 21 2315 19 22 24 25可以观察到我们的搜索是如水一般蔓延开来的,按照我们设置好的搜索规则依次判断.我们设置了一个边长为5X5的图,且初始点我们让其从(1,1)开始进行.过程的简单描述:从(1,1)开始,先判断右边是否走过,没走过将其标为2.然后再回到(1,1)接着判断下面是否走过,没走过将其标为3.然后判断左边,为边界无法走,接着判断上面,为边界无法走.(1,1)此时4个方位都判断完了,接着来到(1,1)这个点判断标记的第一个点———(1,2)然后从(1,2)开始刚刚的过程,最终形成了这个图.题目:快乐的马里奥 这是一个基础的bfs题,题解思路如我们上述相同. 用代码怎么实现呢? 我们需要用到核心为 queue 和 pair 使用队列的特性---先进先出,记录最先标记了的坐标位置,下面给出AC代码#include<iostream> #include<queue> #include<vector> using namespace std; int fx[4]={0,1,0,-1}; int fy[4]={1,0,-1,0}; int main() { std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); int m, n; cin >> m >> n;//输入行列 vector<vector <int> >v( m + 1,vector<int> ( n + 1, 0 ));//设置二维数组 queue<pair<int,int> >q;//队列用来记录坐标 q.push({1,1});//设置初始的坐标,也是开始的坐标 v[1][1] = 1;//对初始点赋初值 int cnt = 2;//因为初始点为1,第二个点从2开始 while(!q.empty()){//队列存储的坐标不为空就执行 //取出队列中存储的第一个坐标,用完就丢 int x = q.front().first; int y = q.front().second; q.pop(); //依次判断四个方位 for(int i = 0;i < 4;i++){ int nx = x + fx[i]; int ny = y + fy[i]; if(nx <= m && nx > 0 && ny <= n && ny > 0 && v[nx][ny] == 0){ v[nx][ny] = cnt++;//赋值标记 q.push({nx,ny});//将赋值点的坐标存入队列 } } } //打印输出 for(int i = 1; i <= m;i++){ for(int j = 1; j <= n;j++){ cout << v[i][j] << " "; } cout << '\n'; } return 0; } -
 (DFS) Depth-First Search入门 Depth-First Search简称DFS,深度优先搜索。深度优先,优先在于深度,尽量往最深处走。原理:从某一节点开始走,若遇到分支,选择某条路冲到底,遇到分支就随便选只管冲冲冲,直到冲到底再无选择,然后按原路返回如果再遇到分支且有没走过的路,依然冲冲冲。直到全部都搜索完。 DFS 就如《葬送的芙莉莲》中芙莉莲与勇者探索迷宫的精神,攻略迷宫要将迷宫全部探索完才是迷宫寻宝的真正魅力!!!如题 【入门】扫地机器人 我们根据题意可以知道n与m的值为2~9,所以二维数组可以开a11即使nm为最大时依然可以在周围留一圈0,反正判断时越界等问题。 根据题意我们需要设置一个判断规则: 按右下左上 的优先级进行判断。下面给出AC代码#include<iostream> #include<vector> using namespace std; const int N = 11;//因为n和m是2~9的数所以周围留下了一圈 int n,m; vector<vector<int> >a(N,vector<int>(N, 0)); //递归深搜 void dfs(int x, int y, int k)//为(x,y)赋k值 { a[x][y] = k; //按照题目要求的右下左上的顺序依次设计判断x与y的加减依次对应了右下左上 if(y + 1 <= m && a[x][y + 1] == 0){ dfs(x, y + 1, k + 1); }else if(x + 1 <= n && a[x + 1][y] == 0){ dfs(x + 1, y, k + 1); }else if(y - 1 > 0 && a[x][y - 1] == 0){ dfs(x, y - 1, k + 1); }else if(x - 1 > 0 && a[x - 1][y] == 0){ dfs(x - 1, y, k + 1); } } int main() { std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); //输入行列 cin >> n >> m; //赋初值 dfs(1, 1, 1);//依题意设计函数dfs为(1,1)赋值为1,dfs函数赋值的点是我们搜索开始的最初点 //输出 for(int i = 1; i <= n; i++){ for(int j = 1; j <= m; j++){ printf("%3d",a[i][j]); } printf("\n"); } }
(DFS) Depth-First Search入门 Depth-First Search简称DFS,深度优先搜索。深度优先,优先在于深度,尽量往最深处走。原理:从某一节点开始走,若遇到分支,选择某条路冲到底,遇到分支就随便选只管冲冲冲,直到冲到底再无选择,然后按原路返回如果再遇到分支且有没走过的路,依然冲冲冲。直到全部都搜索完。 DFS 就如《葬送的芙莉莲》中芙莉莲与勇者探索迷宫的精神,攻略迷宫要将迷宫全部探索完才是迷宫寻宝的真正魅力!!!如题 【入门】扫地机器人 我们根据题意可以知道n与m的值为2~9,所以二维数组可以开a11即使nm为最大时依然可以在周围留一圈0,反正判断时越界等问题。 根据题意我们需要设置一个判断规则: 按右下左上 的优先级进行判断。下面给出AC代码#include<iostream> #include<vector> using namespace std; const int N = 11;//因为n和m是2~9的数所以周围留下了一圈 int n,m; vector<vector<int> >a(N,vector<int>(N, 0)); //递归深搜 void dfs(int x, int y, int k)//为(x,y)赋k值 { a[x][y] = k; //按照题目要求的右下左上的顺序依次设计判断x与y的加减依次对应了右下左上 if(y + 1 <= m && a[x][y + 1] == 0){ dfs(x, y + 1, k + 1); }else if(x + 1 <= n && a[x + 1][y] == 0){ dfs(x + 1, y, k + 1); }else if(y - 1 > 0 && a[x][y - 1] == 0){ dfs(x, y - 1, k + 1); }else if(x - 1 > 0 && a[x - 1][y] == 0){ dfs(x - 1, y, k + 1); } } int main() { std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); //输入行列 cin >> n >> m; //赋初值 dfs(1, 1, 1);//依题意设计函数dfs为(1,1)赋值为1,dfs函数赋值的点是我们搜索开始的最初点 //输出 for(int i = 1; i <= n; i++){ for(int j = 1; j <= m; j++){ printf("%3d",a[i][j]); } printf("\n"); } } -
 二分法 二分查找本质上是按照某一性质每次一分为二查找左右边界 普通的二分查找 题目 题目解释:在一组有序无重复数组中查找某一个数,如果能查找到输出这个数是第几个数,否则输出-1. 我们可以使用二分法进行查找,即将数组一分为二,从中间的数进行判断是否大于或小于我们要查找的数,因为数组是有序递增的,所以如果中间数大于查找的数我们便查找左部分的数否则查找右部分的数。 代码示例:#include<iostream> #include<vector> using namespace std; int main() { std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n; cin >> n; vector<int>a(n + 1); for (int i = 1; i <= n; i++)cin >> a[i]; int l = 1, r = n;//因为数组大小为n所以左右边界为(1,n) int x; cin >> x;//输入要查找的数 while (l < r)//设置跳出循环的条件,即当l=r时退出循环 { int mid = (l + r) >> 1;//(l+r)/2,对中间数进行向下取整 if (a[mid] >= x)r = mid; //如果查询的数小于等于中间数,查询左部分,将右边界向左移 else l = mid + 1; //如果查询的数大于中间数,查询右部分,将左边界向右移,因为数组mid对应的数不对所以再右移一位 } //l下标对应的即是最后的查找 if (a[l] == x) cout << l << '\n'; else cout << -1 << '\n'; return 0; }二分查找左右边界 二分查找左边界 二分查找右边界 题目解释:左右边界意思是最左或最右,或者最小或最大。 如一组数12333445,查找3的左边界,答案为3.查找3的右边界,答案为5二分查找左边界 左边界代码://二分查找左边界 #include<iostream> #include<vector> using namespace std; int main() { std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n; cin >> n; vector<int>a(n + 1); for (int i = 1; i <= n; i++)cin >> a[i]; int y; cin >> y; while (y--) { int x; cin >> x; int l = 1, r = n; while (l < r) { int mid = (l + r) >> 1; if (a[mid] >= x)r = mid; else l = mid + 1; } if (a[l] == x)cout << l << ' '; else cout << -1 << ' '; } return 0; }可以看到查找左边界和普通二分查找原理相同,稍有的不同只是因为题目的需求不同,实际上普通二分查找是查找左右边界的特例,只不过是因为数组中的数是否重复而不同 下面给出右边界代码:#include<iostream> #include<vector> using namespace std; int main() { std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n; cin >> n; vector<int>a(n + 1); for (int i = 1; i <= n; i++)cin >> a[i]; int y; cin >> y; while (y--) { int x; cin >> x; int l = 1, r = n; while (l < r) { int mid = (l + r + 1) >> 1;//1.注意, 如果 l=r-1 && nums[mid] <= target 此时l不能变化,进入死循环因此 mid更新应该改变 ,即 +1 if (a[mid] <= x)l = mid;//2.注意 else r = mid - 1;//注意 } if (a[l] == x)cout << l << ' '; else cout << -1 << ' '; } return 0; }注意代码中的注意,为与左边界不同的地方 1.如果 l=r-1 && nums[mid] <= target 此时l不能变化,进入死循环,因此 mid更新应该改变 ,即 +12.l不能+1,如果r=l+1,可能存在mid =r =l +1让循环进入死循环3.r-1是因为当前mid对应的数不为查找的数查找最小值用左边界,查找最大值用右边界左右边界的不同可以简单记忆为:左加右减二分答案-以伐木工为例 伐木工 咋一看与二分无关,如果直接暴力容易超时,因此使用二分法。 具体思路为写一个check函数判断当前高度以上的数相加是否符合所需的木材 此时的左右边界设置为0与最高高度的树,因为我们需要求的是伐木的高度,因此我们使用的二分法是求右边界,边界范围只与给出树的最高高度有关,再高就不礼貌了。 代码示例#include<iostream> #include<vector> using namespace std; using ll = long long; bool check(ll mid, ll n, ll m, vector<ll>& a) { ll num = 0;//num求a中mid高度以上的树的和 for (ll i = 1; i <= n; i++) { if (a[i] > mid)num += (a[i] - mid); if (num >= m)return true;//如果相加的木材长度大于或等于需要的木材长度,返回true,继续增加高度 } return false; } int main() { std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); ll n, m; cin >> n >> m; vector<ll>a(n + 1); for (ll i = 1; i <= n; i++)cin >> a[i]; ll l = 0;//左边界 //找出最高的树作为右边边界 ll r = a[0]; for (ll i = 1; i <= n; i++) r = max(r, a[i]); //二分查找右边界 while (l < r) { ll mid = (l + r + 1) >> 1; if (check(mid, n, m, a)) l = mid; else r = mid - 1; } cout << l << '\n'; return 0; }洛谷-进击的奶牛 题解 本题查找相邻两头牛 最大 的最近距离,因此使用 右边界 选择好使用哪种二分后想想该怎么具体实现。我们想要对首先我们需要对输入的数组进行排序,然后取 l 为 1 , r 为一个很大的值即可。 check 函数中我们需要定义一个 num 对间隔距离进行求和,当 num>=mid 时对牛牛数量进行加 1 并且让 num为0 ,重新计数,直到牛牛的数量 >= 输入的奶牛的数量 c 。 示例代码//洛谷 进击的奶牛 #include<iostream> #include<vector> #include<algorithm> using namespace std; const int N=0x3f3f3f3f; using ll = long long; ll n, c; vector<ll>a(1); bool check(ll mid){ ll num = 0; ll nn = 1; for(ll i = 2; i <= n; i++){ num += a[i] - a[i - 1]; if(num >= mid) { nn++; num = 0; } if(nn >= c) return true; } return false; } int main() { std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); cin >> n >> c; a.resize(n + 1); for(ll i = 1;i <= n; i++) cin >> a[i]; sort(a.begin(), a.end()); ll l = 0,r = N; while(l < r){ ll mid = (l + r + 1) >> 1; if(check(mid)) l = mid; else r = mid - 1; } cout << l <<'\n'; return 0; }
二分法 二分查找本质上是按照某一性质每次一分为二查找左右边界 普通的二分查找 题目 题目解释:在一组有序无重复数组中查找某一个数,如果能查找到输出这个数是第几个数,否则输出-1. 我们可以使用二分法进行查找,即将数组一分为二,从中间的数进行判断是否大于或小于我们要查找的数,因为数组是有序递增的,所以如果中间数大于查找的数我们便查找左部分的数否则查找右部分的数。 代码示例:#include<iostream> #include<vector> using namespace std; int main() { std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n; cin >> n; vector<int>a(n + 1); for (int i = 1; i <= n; i++)cin >> a[i]; int l = 1, r = n;//因为数组大小为n所以左右边界为(1,n) int x; cin >> x;//输入要查找的数 while (l < r)//设置跳出循环的条件,即当l=r时退出循环 { int mid = (l + r) >> 1;//(l+r)/2,对中间数进行向下取整 if (a[mid] >= x)r = mid; //如果查询的数小于等于中间数,查询左部分,将右边界向左移 else l = mid + 1; //如果查询的数大于中间数,查询右部分,将左边界向右移,因为数组mid对应的数不对所以再右移一位 } //l下标对应的即是最后的查找 if (a[l] == x) cout << l << '\n'; else cout << -1 << '\n'; return 0; }二分查找左右边界 二分查找左边界 二分查找右边界 题目解释:左右边界意思是最左或最右,或者最小或最大。 如一组数12333445,查找3的左边界,答案为3.查找3的右边界,答案为5二分查找左边界 左边界代码://二分查找左边界 #include<iostream> #include<vector> using namespace std; int main() { std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n; cin >> n; vector<int>a(n + 1); for (int i = 1; i <= n; i++)cin >> a[i]; int y; cin >> y; while (y--) { int x; cin >> x; int l = 1, r = n; while (l < r) { int mid = (l + r) >> 1; if (a[mid] >= x)r = mid; else l = mid + 1; } if (a[l] == x)cout << l << ' '; else cout << -1 << ' '; } return 0; }可以看到查找左边界和普通二分查找原理相同,稍有的不同只是因为题目的需求不同,实际上普通二分查找是查找左右边界的特例,只不过是因为数组中的数是否重复而不同 下面给出右边界代码:#include<iostream> #include<vector> using namespace std; int main() { std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); int n; cin >> n; vector<int>a(n + 1); for (int i = 1; i <= n; i++)cin >> a[i]; int y; cin >> y; while (y--) { int x; cin >> x; int l = 1, r = n; while (l < r) { int mid = (l + r + 1) >> 1;//1.注意, 如果 l=r-1 && nums[mid] <= target 此时l不能变化,进入死循环因此 mid更新应该改变 ,即 +1 if (a[mid] <= x)l = mid;//2.注意 else r = mid - 1;//注意 } if (a[l] == x)cout << l << ' '; else cout << -1 << ' '; } return 0; }注意代码中的注意,为与左边界不同的地方 1.如果 l=r-1 && nums[mid] <= target 此时l不能变化,进入死循环,因此 mid更新应该改变 ,即 +12.l不能+1,如果r=l+1,可能存在mid =r =l +1让循环进入死循环3.r-1是因为当前mid对应的数不为查找的数查找最小值用左边界,查找最大值用右边界左右边界的不同可以简单记忆为:左加右减二分答案-以伐木工为例 伐木工 咋一看与二分无关,如果直接暴力容易超时,因此使用二分法。 具体思路为写一个check函数判断当前高度以上的数相加是否符合所需的木材 此时的左右边界设置为0与最高高度的树,因为我们需要求的是伐木的高度,因此我们使用的二分法是求右边界,边界范围只与给出树的最高高度有关,再高就不礼貌了。 代码示例#include<iostream> #include<vector> using namespace std; using ll = long long; bool check(ll mid, ll n, ll m, vector<ll>& a) { ll num = 0;//num求a中mid高度以上的树的和 for (ll i = 1; i <= n; i++) { if (a[i] > mid)num += (a[i] - mid); if (num >= m)return true;//如果相加的木材长度大于或等于需要的木材长度,返回true,继续增加高度 } return false; } int main() { std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); ll n, m; cin >> n >> m; vector<ll>a(n + 1); for (ll i = 1; i <= n; i++)cin >> a[i]; ll l = 0;//左边界 //找出最高的树作为右边边界 ll r = a[0]; for (ll i = 1; i <= n; i++) r = max(r, a[i]); //二分查找右边界 while (l < r) { ll mid = (l + r + 1) >> 1; if (check(mid, n, m, a)) l = mid; else r = mid - 1; } cout << l << '\n'; return 0; }洛谷-进击的奶牛 题解 本题查找相邻两头牛 最大 的最近距离,因此使用 右边界 选择好使用哪种二分后想想该怎么具体实现。我们想要对首先我们需要对输入的数组进行排序,然后取 l 为 1 , r 为一个很大的值即可。 check 函数中我们需要定义一个 num 对间隔距离进行求和,当 num>=mid 时对牛牛数量进行加 1 并且让 num为0 ,重新计数,直到牛牛的数量 >= 输入的奶牛的数量 c 。 示例代码//洛谷 进击的奶牛 #include<iostream> #include<vector> #include<algorithm> using namespace std; const int N=0x3f3f3f3f; using ll = long long; ll n, c; vector<ll>a(1); bool check(ll mid){ ll num = 0; ll nn = 1; for(ll i = 2; i <= n; i++){ num += a[i] - a[i - 1]; if(num >= mid) { nn++; num = 0; } if(nn >= c) return true; } return false; } int main() { std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); cin >> n >> c; a.resize(n + 1); for(ll i = 1;i <= n; i++) cin >> a[i]; sort(a.begin(), a.end()); ll l = 0,r = N; while(l < r){ ll mid = (l + r + 1) >> 1; if(check(mid)) l = mid; else r = mid - 1; } cout << l <<'\n'; return 0; }