高精度运算(加减乘除)

在程序中高精度加法和高精度减法的运算本质是模拟我们在小学就学过的运算规则，也是我们平时用的运算规则：相加大于10就进1，相减小于就向高位借.

高精度加法

//高精度加法
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
//a,b字符串用于存入两个大数
std::string a, b;
//m,n分别逆序存入a,b
std::vector <int> m, n, p;
//la,lb用于记录a,b的位数
int la, lb;

void highPrecisionAddition() {
    int sum = 0;
    for (int i = 0; i < la || i < lb; i++) {
        if (i < la) {
            sum += m[i];
        }
        if (i < lb) {
            sum += n[i];
        }
        p.push_back(sum % 10);
        sum /= 10;
    }
    if (sum) {
        p.push_back(sum);
    }
}

int main() {
    //以字符串形式存放
    std::cin >> a;
    std::cin >> b;
    la = a.size();
    lb = b.size();
    //将字符串按位逆序存入数组m, n
    for (int i = la - 1; i >= 0; i--) {
        m.push_back(a[i] - '0');
    }
    for (int i = lb - 1; i >= 0; i--) {
        n.push_back(b[i] - '0');
    }
    highPrecisionAddition();
    reverse(p.begin(), p.end());
    for (auto i : p) {
        std::cout << i;
    }
    return 0;
}

高精度减法

//高精度减法
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>

std::string a, b;
std::vector <int> m, n, p;
int la, lb;

bool cmp() {
    if (la != lb) {
        return la > lb;
    }
    for (int i = la - 1; i >= 0; i--) {
        if (m[i] != n[i]) {
            return m[i] > n[i];
        }
    }
    return true;
} 


void highPrecisionSubtraction(std::vector <int> &m, std::vector <int> &n) {
    int sub = 0;
    for (int i = 0; i < la || i < lb; i++) {
        sub = m[i];
        if (i < lb) {
            sub -= n[i];
        }
        if (sub < 0) {
            m[i + 1]--;
            sub += 10;
        }
        p.push_back(sub);
    }
    //去除前面多余的零，保证输出时前面不出现零
    while (p.size() > 1 && !p.back()) {
        p.pop_back();
    }
}


int main () {
    std::cin >> a;
    std::cin >> b;
    
    la = a.size();
    lb = b.size();

    for (int i = la - 1; i >= 0; i--) {
        m.push_back(a[i] - '0');
    }
    for (int i = lb - 1; i >= 0; i--) {
        n.push_back(b[i] - '0');
    }

    //如果输入是小减大则需要输出负号
    if (!cmp()) {
        //保证highPrecisionSubtraction里是大减小
        std::swap(m, n);
        std::cout << "-";
    }

    highPrecisionSubtraction(m, n);

    reverse(p.begin(), p.end());
    for (auto i : p) {
        std::cout << i;
    }
    return 0;
}

高精度乘法
在程序中的高精度乘法也与我们平时的运算差不多，略有不同.

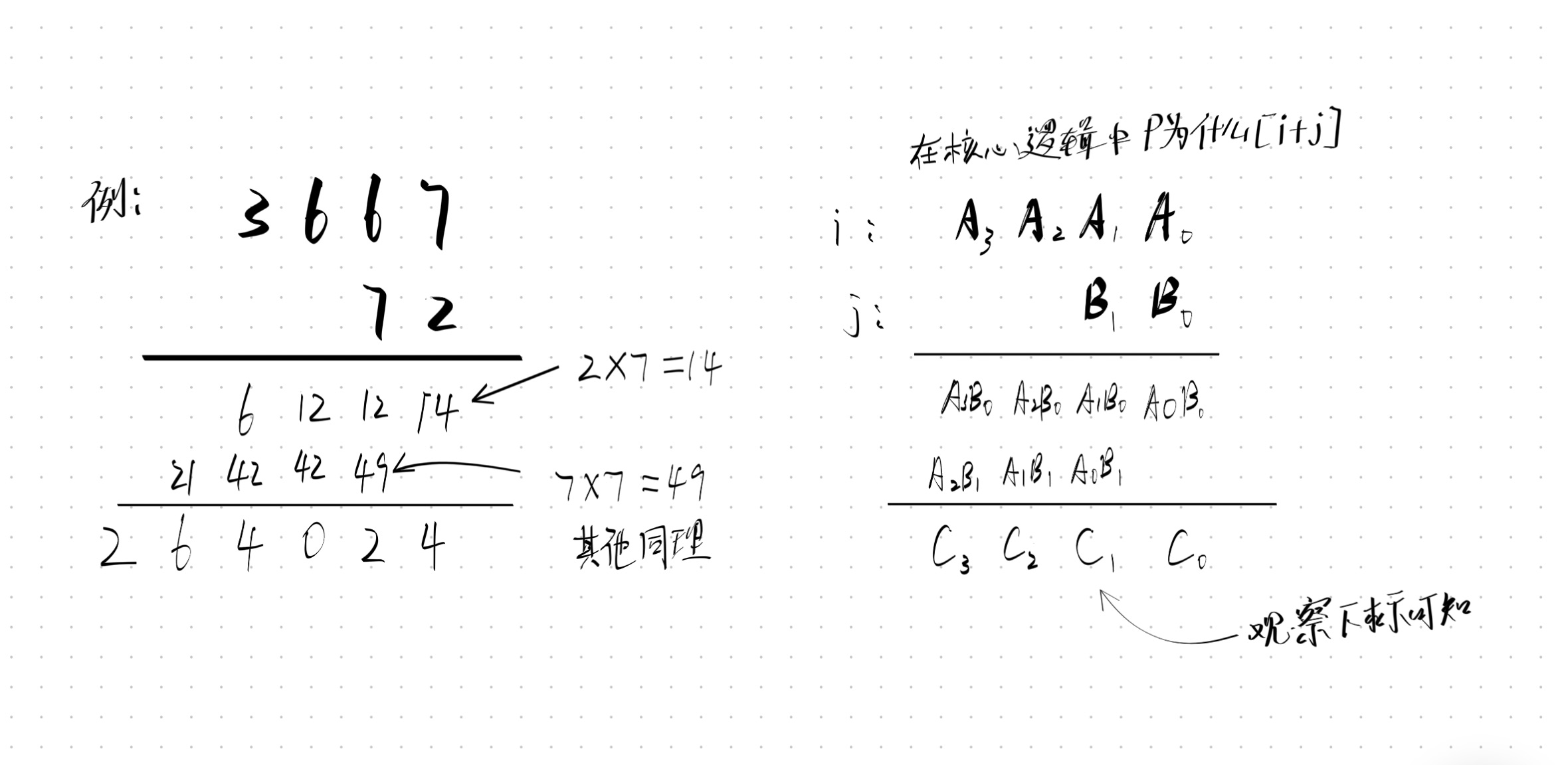
//高精度乘法
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
std::string a, b;
std::vector <int> m, n;
int la, lb;

void highPrecisionMultiplication(std::vector <int>& p) {
    for (int i = 0; i < la; i++) {
        for (int j = 0; j < lb; j++) {
            p[i + j] += m[i] * n[j];
            p[i + j + 1] += p[i + j] / 10;
            p[i + j] %= 10;
        }
    }
    while (p.size() > 1 && !p.back()) {
        p.pop_back();
    }
}

int main() {
    std::cin >> a;
    std::cin >> b;

    la = a.size();
    lb = b.size();
    std::vector <int> p(la + lb);

    for (int i = la - 1; i >= 0; i--) {
        m.push_back(a[i] - '0');
    }
    for (int i = lb - 1; i >= 0; i--) {
        n.push_back(b[i] - '0');
    }

    highPrecisionMultiplication(p);

    std::reverse(p.begin(), p.end());
    for (auto i : p) {
        std::cout << i;
    }
    return 0;
}

高精度除法
高精度除法的被除数为大数，而除数相对较小在整型范围内
运算规则同平时在纸上所列的计算方法

#include <iostream>
#include <string>
#include <vector>

std::string a;
int n;
std::vector <int> m, p;
int la, lb;

void highPrecisionDivision() {
    long long r = 0;
    for (int i = la - 1; i >= 0; i--) {
        r = r * 10 + m[i];
        p.push_back(r / n);
        r %= n;
    }
    while (p.size() > 1 && !p.back()) {
        p.pop_back();
    }
}

int main () {
    std::cin >> a;
    std::cin >> n;
    la = a.size();

    for (int i = la - 1; i >= 0; i--) {
        m.push_back(a[i] - '0');
    }

    highPrecisionDivision();

    for (auto i : p) {
        std::cout << i;
    }
    return 0;
}