二叉树的建立与遍历

二叉树是一种非线性数据结构.
二叉树 由节点构成,每个节点包含节点值和指向左节点和右节点的指针.

常用术语:
根节点（root node）：位于二叉树顶层的节点，没有父节点。
叶节点（leaf node）：没有子节点的节点，其两个指针均指向 None 。
边（edge）：连接两个节点的线段，即节点引用（指针）。
节点所在的层（level）：从顶至底递增，根节点所在层为 1 。
节点的度（degree）：节点的子节点的数量。在二叉树中，度的取值范围是 0、1、2 。
二叉树的高度（height）：从根节点到最远叶节点所经过的边的数量。
节点的深度（depth）：从根节点到该节点所经过的边的数量。
节点的高度（height）：从距离该节点最远的叶节点到该节点所经过的边的数量。

二叉树的遍历 分为层序遍历,前序遍历,中序遍历,后序遍历.
层序遍历本质为BFS,即广度优先搜索.
层序遍历顾名思义,为一层层的从上往下,从左到右遍历.

前序遍历,中序遍历,后序遍历本质为DFS,即深度优先搜索.
访问时机如图:

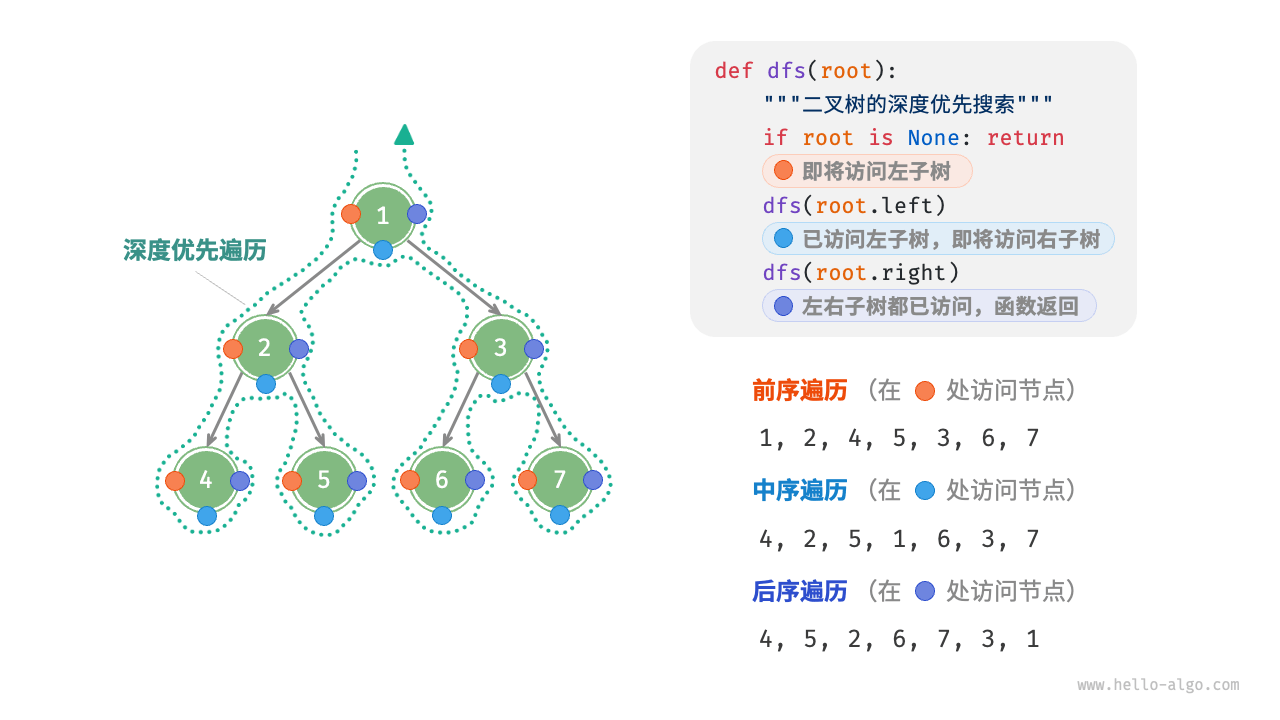
代码示例:

#include<vector>
#include<queue>
#include<iostream>
struct tree{
    int value;
    tree *left;
    tree *right;
    tree(int x) : value(x), left(nullptr), right(nullptr){}
};
std::vector<int> vec;
//层序遍历
std::vector<int> levelorder(tree *root){
    std::queue<tree *> q;
    q.push(root);
    std::vector<int> vec;
    while(!q.empty()){
        tree *node = q.front();
        q.pop();
        vec.push_back(node->value);
        if(node->left != nullptr){
            q.push(node->left);
        }
        if(node->right != nullptr){
            q.push(node->right);
        }
    }
    return vec;
}
//前序遍历
void preorder(tree *root){
    if(root == nullptr){
        return;
    }
    vec.push_back(root->value);
    preorder(root->left);
    preorder(root->right);
}
//中序遍历
void inorder(tree *root){
    if(root == nullptr){
        return;
    }
    inorder(root->left);
    vec.push_back(root->value);
    inorder(root->right);
}
//后序遍历
void postorder(tree *root){
    if(root == nullptr){
        return;
    }
    postorder(root->left);
    postorder(root->right);
    vec.push_back(root->value);
}

int main(){
    tree *t0 = new tree(1);
    tree *t1 = new tree(2);
    tree *t2 = new tree(3);
    tree *t3 = new tree(4);
    tree *t4 = new tree(5);

    t0->left = t1;
    t0->right = t2;
    t1->left = t3;
    t1->right = t4;
    
    preorder(t0);
    for(auto &i : vec){
        std::cout << i << " ";
    }
    std::cout << std::endl;
    vec.clear();

    inorder(t0);
    for(auto &i : vec){
        std::cout << i << " ";
    }
    std::cout << std::endl;
    vec.clear();  

    postorder(t0);
    for(auto &i : vec){
        std::cout << i << " ";
    }
    std::cout << std::endl;
    vec.clear();

    return 0;
}

使用数组表示二叉树:
用数组表示时,观察可知节点下标为 i 时,
父节点下标为 (i - 1) / 2
左节点下标为 2 i + 1 ,右节点下标为 2 i + 2
依此规律我们可以使用数组表示出二叉树

#include<vector>
#include<iostream>
std::vector<int> vec;

int parent(int i){
    return (i - 1) / 2;
}
int left(int i){
    return 2 * i + 1;
}
int right(int i){
    return 2 * i + 2;
}


void pretree(std::vector<int> &tree, int i){
    if(i < 0 || i >= tree.size()){
        return;
    }
    vec.push_back(tree[i]);
    pretree(tree, left(i));
    pretree(tree, right(i));
}
void intree(std::vector<int> &tree, int i){
    if(i < 0 || i >= tree.size()){
        return;
    }
    intree(tree, left(i));
    vec.push_back(tree[i]);
    intree(tree, right(i));
}
void posttree(std::vector<int> &tree, int i){
    if(i < 0 || i >= tree.size()){
        return;
    }
    posttree(tree, left(i));
    posttree(tree, right(i));
    vec.push_back(tree[i]);
}

int main(){
    std::vector<int> tree(10);
    for(int i = 0; i < 10; i++){
        std::cin >> tree[i];
    }

    pretree(tree, 0);
    for(auto &i : vec){
        std::cout << i << " ";
    }
    std::cout << std::endl;
    vec.clear();

    intree(tree, 0);
    for(auto &i : vec){
        std::cout << i << " ";
    }
    std::cout << std::endl;
    vec.clear();

    posttree(tree, 0);
    for(auto &i : vec){
        std::cout << i << " ";
    }
    std::cout << std::endl;
    vec.clear();

    return 0;
}

参考文章