二分法

二分查找本质上是按照某一性质每次一分为二查找左右边界
普通的二分查找
题目
题目解释:在一组有序无重复数组中查找某一个数，如果能查找到输出这个数是第几个数，否则输出-1.
我们可以使用二分法进行查找，即将数组一分为二，从中间的数进行判断是否大于或小于我们要查找的数，因为数组是有序递增的，所以如果中间数大于查找的数我们便查找左部分的数否则查找右部分的数。
代码示例:

#include<iostream>
#include<vector>
using namespace std;
int main()
{
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n; cin >> n;
    vector<int>a(n + 1);
    for (int i = 1; i <= n; i++)cin >> a[i];

    int l = 1, r = n;//因为数组大小为n所以左右边界为(1,n)
    int x; cin >> x;//输入要查找的数
    while (l < r)//设置跳出循环的条件，即当l=r时退出循环
    {
        int mid = (l + r) >> 1;//(l+r)/2,对中间数进行向下取整
        if (a[mid] >= x)r = mid; //如果查询的数小于等于中间数，查询左部分，将右边界向左移
        else l = mid + 1; //如果查询的数大于中间数，查询右部分，将左边界向右移，因为数组mid对应的数不对所以再右移一位
    }
    //l下标对应的即是最后的查找
    if (a[l] == x) cout << l << '\n';
    else cout << -1 << '\n';
    return 0;
}

二分查找左右边界
二分查找左边界
二分查找右边界
题目解释:左右边界意思是最左或最右，或者最小或最大。
如一组数12333445，查找3的左边界，答案为3.查找3的右边界，答案为5

二分查找左边界
左边界代码:

//二分查找左边界
#include<iostream>
#include<vector>
using namespace std;
int main()
{
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n; cin >> n;
    vector<int>a(n + 1);
    for (int i = 1; i <= n; i++)cin >> a[i];

    int y; cin >> y;
    while (y--) {
        int x; cin >> x;
        int l = 1, r = n;
        while (l < r) {
            int mid = (l + r) >> 1;
            if (a[mid] >= x)r = mid;
            else l = mid + 1;
        }
        if (a[l] == x)cout << l << ' ';
        else cout << -1 << ' ';
    }
    return 0;
}

可以看到查找左边界和普通二分查找原理相同，稍有的不同只是因为题目的需求不同，实际上普通二分查找是查找左右边界的特例，只不过是因为数组中的数是否重复而不同
下面给出右边界代码:

#include<iostream>
#include<vector>
using namespace std;
int main()
{
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n; cin >> n;
    vector<int>a(n + 1);
    for (int i = 1; i <= n; i++)cin >> a[i];

    int y; cin >> y;
    while (y--) {
        int x; cin >> x;
        int l = 1, r = n;
        while (l < r) {
            int mid = (l + r + 1) >> 1;//1.注意， 如果 l=r-1 && nums[mid] <= target 此时l不能变化，进入死循环因此 mid更新应该改变 ，即 +1
            if (a[mid] <= x)l = mid;//2.注意
            else r = mid - 1;//注意
        }
        if (a[l] == x)cout << l << ' ';
        else cout << -1 << ' ';
    }
    return 0;
}

注意代码中的注意，为与左边界不同的地方
1.如果 l=r-1 && nums[mid] <= target 此时l不能变化，进入死循环，因此 mid更新应该改变 ，即 +1
2.l不能+1,如果r=l+1，可能存在mid =r =l +1让循环进入死循环
3.r-1是因为当前mid对应的数不为查找的数

查找最小值用左边界，查找最大值用右边界
左右边界的不同可以简单记忆为:左加右减

二分答案-以伐木工为例
伐木工
咋一看与二分无关，如果直接暴力容易超时，因此使用二分法。
具体思路为写一个check函数判断当前高度以上的数相加是否符合所需的木材
此时的左右边界设置为0与最高高度的树，因为我们需要求的是伐木的高度，因此我们使用的二分法是求右边界，边界范围只与给出树的最高高度有关，再高就不礼貌了。
代码示例

#include<iostream>
#include<vector>
using namespace std;
using ll = long long;

bool check(ll mid, ll n, ll m, vector<ll>& a)
{
    ll num = 0;//num求a中mid高度以上的树的和
    for (ll i = 1; i <= n; i++) {
        if (a[i] > mid)num += (a[i] - mid);
        if (num >= m)return true;//如果相加的木材长度大于或等于需要的木材长度，返回true，继续增加高度
    }
    return false;
}
int main()
{
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    ll n, m; cin >> n >> m;
    vector<ll>a(n + 1);
    for (ll i = 1; i <= n; i++)cin >> a[i];

    ll l = 0;//左边界
    //找出最高的树作为右边边界
    ll r = a[0];
    for (ll i = 1; i <= n; i++) r = max(r, a[i]);

    //二分查找右边界
    while (l < r) {
        ll mid = (l + r + 1) >> 1;
        if (check(mid, n, m, a)) l = mid;
        else r = mid - 1;
    }
    cout << l << '\n';
    return 0;
}

洛谷-进击的奶牛
题解
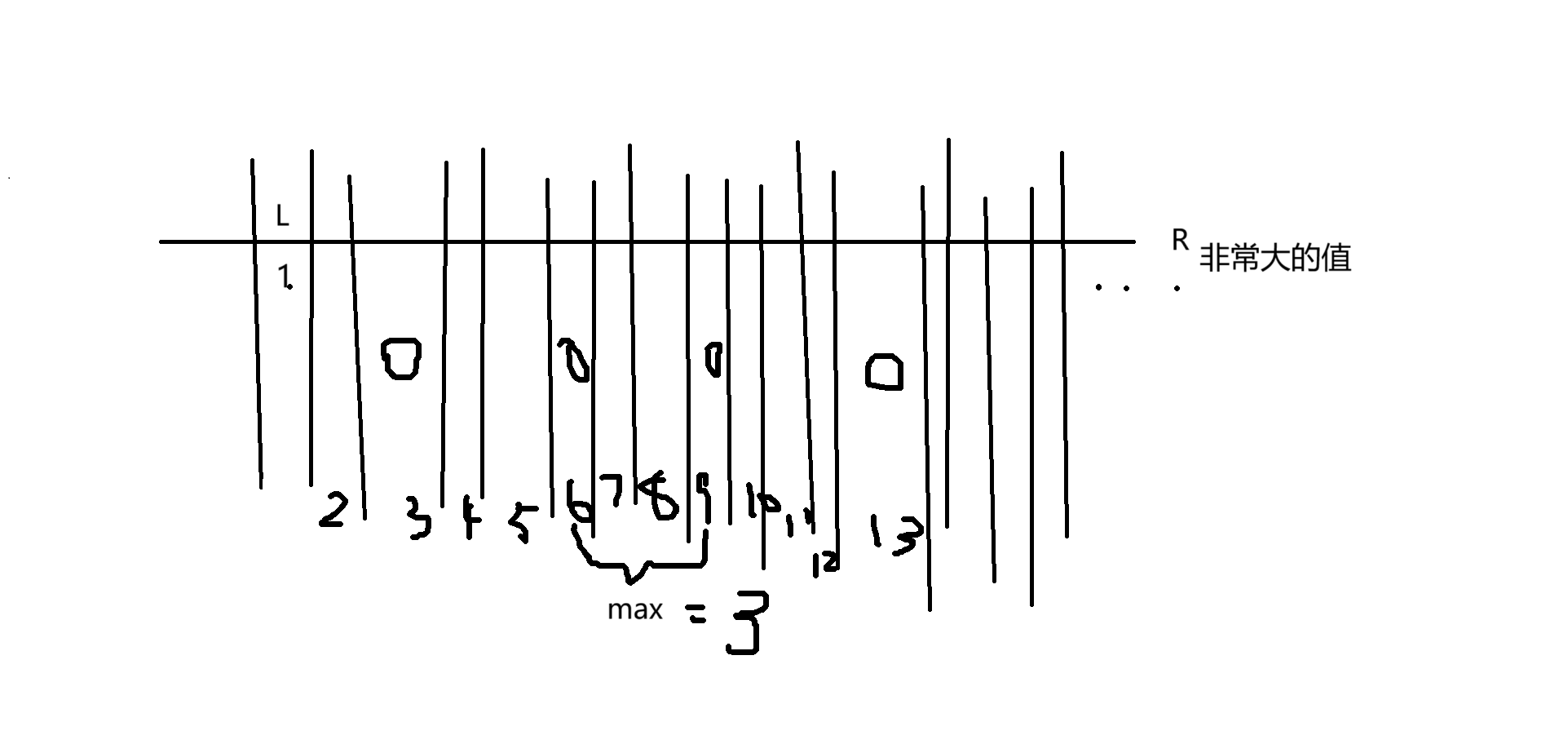
本题查找相邻两头牛 最大 的最近距离，因此使用 右边界
选择好使用哪种二分后想想该怎么具体实现。我们想要对首先我们需要对输入的数组进行排序，然后取 l 为 1 ， r 为一个很大的值即可。 check 函数中我们需要定义一个 num 对间隔距离进行求和，当 num>=mid 时对牛牛数量进行加 1 并且让 num为0 ，重新计数，直到牛牛的数量 >= 输入的奶牛的数量 c 。

示例代码

//洛谷 进击的奶牛
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N=0x3f3f3f3f;
using ll = long long;

ll n, c;
vector<ll>a(1);

bool check(ll mid){
    ll num = 0;
    ll nn = 1;
    for(ll i = 2; i <= n; i++){
        num += a[i] - a[i - 1];
        if(num >= mid) {
            nn++;
            num = 0;
        }
        if(nn >= c) return true;
    }
    return false;
}

int main()
{
    std::ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin >> n >> c;
    a.resize(n + 1);
    for(ll i = 1;i <= n; i++) cin >> a[i];
    sort(a.begin(), a.end());

    ll l = 0,r = N;
    while(l < r){
        ll mid = (l + r + 1) >> 1;
        if(check(mid)) l = mid;
        else r = mid - 1;
    }
    cout << l <<'\n';
    return 0;
}